Vzorec pro oblast pravidelné čtyřúhelníkové pyramidy. Pyramida. Vzorce a vlastnosti pyramidy

Jaké postavě říkáme pyramida? Za prvé je to mnohostěn. Za druhé, na základně tohoto mnohostěnu je libovolný mnohoúhelník a strany pyramidy (boční plochy) mají nutně tvar trojúhelníků sbíhajících se v jednom společném vrcholu. Nyní, když jsme pochopili termín, pojďme zjistit, jak najít povrch pyramidy.

Je zřejmé, že povrchová plocha takového geometrického tělesa je tvořena součtem ploch základny a celého jejího bočního povrchu.

Výpočet plochy základny pyramidy

Volba výpočtového vzorce závisí na tvaru mnohoúhelníku pod naší pyramidou. Může být pravidelný, to znamená se stejně dlouhými stranami, nebo nepravidelný. Zvažme obě možnosti.

Základem je pravidelný mnohoúhelník

Ze školního kurzu víme:

• plocha čtverce se bude rovnat délce jeho strany na druhou;
• Plocha rovnostranného trojúhelníku se rovná čtverci jeho strany dělené 4 a vynásobené druhou odmocninou ze tří.

Existuje však také obecný vzorec pro výpočet plochy jakéhokoli pravidelného mnohoúhelníku (Sn): musíte vynásobit obvod tohoto mnohoúhelníku (P) poloměrem kruhu vepsaného do něj (r) a poté rozdělit výsledek o dva: Sn=1/2P*r .

Na základně je nepravidelný mnohoúhelník

Schéma pro nalezení jeho oblasti je nejprve rozdělit celý mnohoúhelník na trojúhelníky, vypočítat plochu každého z nich pomocí vzorce: 1/2a*h (kde a je základna trojúhelníku, h je výška snížená na tento základ), sečtěte všechny výsledky.

Boční povrch pyramidy

Nyní vypočítejme plochu bočního povrchu pyramidy, tj. součet ploch všech jeho bočních stran. Zde jsou také 2 možnosti.

1. Mějme libovolnou pyramidu, tzn. jeden s nepravidelným mnohoúhelníkem na jeho základně. Poté byste měli vypočítat plochu každé tváře zvlášť a přidat výsledky. Protože strany pyramidy mohou být podle definice pouze trojúhelníky, výpočet se provádí pomocí výše uvedeného vzorce: S=1/2a*h.
2. Ať je naše pyramida správná, tzn. na jeho základně leží pravidelný mnohoúhelník a průmět vrcholu pyramidy je v jeho středu. Poté pro výpočet plochy boční plochy (Sb) stačí najít polovinu součinu obvodu základního polygonu (P) a výšky (h) boční strany (stejnou pro všechny plochy ): Sb = 1/2 P*h. Obvod mnohoúhelníku se určí sečtením délek všech jeho stran.

Celková plocha pravidelné pyramidy se zjistí sečtením plochy její základny s plochou celého bočního povrchu.

Příklady

Pojďme například algebraicky vypočítat povrchy několika pyramid.

Povrchová plocha trojúhelníkové pyramidy

Na základně takové pyramidy je trojúhelník. Pomocí vzorce So=1/2a*h najdeme plochu základny. Stejný vzorec použijeme k nalezení oblasti každé plochy pyramidy, která má také trojúhelníkový tvar, a dostaneme 3 oblasti: S1, S2 a S3. Plocha boční plochy pyramidy je součtem všech ploch: Sb = S1+ S2+ S3. Sečtením ploch stran a základny získáme celkový povrch požadované pyramidy: Sp= So+ Sb.

Povrchová plocha čtyřbokého jehlanu

Plocha bočního povrchu je součtem 4 členů: Sb = S1+ S2+ S3+ S4, z nichž každý se vypočítá pomocí vzorce pro plochu trojúhelníku. A oblast základny bude třeba hledat v závislosti na tvaru čtyřúhelníku - pravidelné nebo nepravidelné. Celková plocha pyramidy se opět získá sečtením plochy základny a celkové plochy dané pyramidy.

Celková plocha boční plochy pyramidy se skládá ze součtu ploch jejích bočních ploch.

Ve čtyřboké pyramidě jsou dva typy ploch - čtyřúhelník na základně a trojúhelníky se společným vrcholem, které tvoří boční plochu.
Nejprve musíte vypočítat plochu bočních ploch. K tomu můžete použít vzorec pro plochu trojúhelníku nebo můžete také použít vzorec pro plochu čtyřúhelníkové pyramidy (pouze pokud je mnohostěn pravidelný). Je-li pyramida pravidelná a je známa délka hrany a základny a k ní nakreslená apotéma h, pak:

Pokud je podle podmínek zadána délka hrany c pravidelného jehlanu a délka strany podstavy a, můžete hodnotu zjistit pomocí následujícího vzorce:

Pokud je uvedena délka hrany na základně a ostrý úhel proti ní nahoře, pak lze plochu bočního povrchu vypočítat poměrem druhé mocniny strany a k dvojitému kosinusu poloviny úhel α:

Uvažujme příklad výpočtu povrchové plochy čtyřúhelníkové pyramidy přes boční hranu a stranu základny.

Problém: Nechť je dán pravidelný čtyřboký jehlan. Délka hrany b = 7 cm, délka strany základny a = 4 cm. Uvedené hodnoty dosaďte do vzorce:

Ukázali jsme výpočty plochy jedné boční plochy pro pravidelnou pyramidu. Respektive. Chcete-li najít plochu celého povrchu, musíte výsledek vynásobit počtem ploch, to znamená 4. Pokud je pyramida libovolná a její plochy se navzájem nerovnají, je třeba vypočítat plochu pro každou jednotlivou stranu. Pokud je základna obdélník nebo rovnoběžník, pak stojí za to pamatovat si jejich vlastnosti. Strany těchto obrazců jsou rovnoběžné ve dvojicích a podle toho budou strany pyramidy také ve dvojicích identické.
Vzorec pro oblast základny čtyřúhelníkové pyramidy přímo závisí na tom, který čtyřúhelník leží na základně. Pokud je pyramida správná, pak se plocha základny vypočítá pomocí vzorce, pokud je základna kosočtverec, budete si muset pamatovat, jak se nachází. Pokud je na základně obdélník, bude nalezení jeho oblasti poměrně jednoduché. Stačí znát délky stran základny. Podívejme se na příklad výpočtu plochy základny čtyřúhelníkové pyramidy.

Úloha: Nechť je dán jehlan, na jehož základně leží obdélník o stranách a = 3 cm, b = 5 cm, z vrcholu jehlanu na každou ze stran se spustí apotéma. h-a = 4 cm, h-b = 6 cm Vrchol jehlanu leží na stejné čáře jako průsečík úhlopříček. Najděte celkovou plochu pyramidy.
Vzorec pro oblast čtyřúhelníkové pyramidy se skládá ze součtu ploch všech ploch a plochy základny. Nejprve najdeme oblast základny:


Nyní se podívejme na strany pyramidy. Ve dvojicích jsou totožné, protože výška jehlanu protíná průsečík úhlopříček. To znamená, že v naší pyramidě jsou dva trojúhelníky se základnou a a výškou h-a a také dva trojúhelníky se základnou b a výškou h-b. Nyní najdeme oblast trojúhelníku pomocí známého vzorce:


Nyní provedeme příklad výpočtu plochy čtyřúhelníkové pyramidy. V naší pyramidě s obdélníkem na základně by vzorec vypadal takto:

Povrchová plocha pyramidy. V tomto článku se podíváme na problémy s pravidelnými pyramidami. Připomínám, že pravidelná pyramida je pyramida, jejíž základna je pravidelný mnohoúhelník, vrchol jehlanu se promítá do středu tohoto mnohoúhelníku.

Boční stěna takové pyramidy je rovnoramenný trojúhelník.Výška tohoto trojúhelníku nakresleného od vrcholu pravidelné pyramidy se nazývá apotém, SF - apotém:

V níže uvedeném typu problému musíte najít povrchovou plochu celé pyramidy nebo oblast jejího bočního povrchu. Blog již pojednával o několika problémech s pravidelnými pyramidami, kde byl dotaz na nalezení prvků (výška, hrana základny, boční hrana).

Úkoly jednotné státní zkoušky obvykle zkoumají pravidelné trojúhelníkové, čtyřúhelníkové a šestihranné jehlany. U pravidelných pětiúhelníkových a sedmibokých pyramid jsem žádné problémy nezaznamenal.

Vzorec pro plochu celého povrchu je jednoduchý - musíte najít součet plochy základny pyramidy a plochy jejího bočního povrchu:

Podívejme se na úkoly:

Strany základny pravidelné čtyřboké pyramidy jsou 72, boční hrany jsou 164. Najděte plochu této pyramidy.

Plocha povrchu pyramidy se rovná součtu ploch boční plochy a základny:

*Boční plocha se skládá ze čtyř trojúhelníků o stejné ploše. Základem pyramidy je čtverec.

Plochu strany pyramidy můžeme vypočítat pomocí:

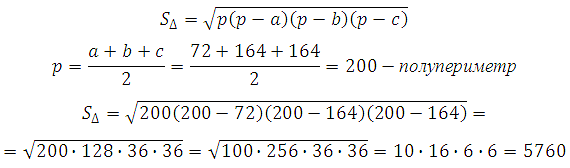
Povrch pyramidy je tedy:

Odpověď: 28224

Strany základny pravidelné šestihranné pyramidy se rovnají 22, boční hrany jsou rovny 61. Najděte boční povrch této pyramidy.

Základem pravidelného šestibokého jehlanu je pravidelný šestiúhelník.

Boční plocha této pyramidy se skládá ze šesti oblastí stejných trojúhelníků se stranami 61, 61 a 22:

Pojďme najít oblast trojúhelníku pomocí Heronova vzorce:

Boční povrch je tedy:

Odpověď: 3240

*Ve výše uvedených problémech lze oblast boční plochy najít pomocí jiného trojúhelníkového vzorce, ale k tomu musíte vypočítat apotém.

27155. Najděte plochu pravidelného čtyřbokého jehlanu, jehož základní strany jsou 6 a jehož výška je 4.

Abychom našli plochu pyramidy, potřebujeme znát plochu základny a plochu boční plochy:

Plocha základny je 36, protože se jedná o čtverec se stranou 6.

Boční plocha se skládá ze čtyř ploch, což jsou stejné trojúhelníky. Abyste našli oblast takového trojúhelníku, musíte znát jeho základnu a výšku (apotém):

* Plocha trojúhelníku se rovná polovině součinu základny a výšky k této základně.

Základ je známý, rovná se šest. Zjistíme výšku. Zvažte pravoúhlý trojúhelník (zvýrazněný žlutě):

Jedna noha se rovná 4, protože toto je výška pyramidy, druhá je rovna 3, protože se rovná polovině hrany základny. Můžeme najít přeponu pomocí Pythagorovy věty:

To znamená, že plocha bočního povrchu pyramidy je:

Povrchová plocha celé pyramidy je tedy:

Odpověď: 96

27069. Strany základny pravidelného čtyřbokého jehlanu se rovnají 10, boční hrany se rovnají 13. Najděte plochu tohoto jehlanu.

27070. Strany základny pravidelného šestibokého jehlanu se rovnají 10, boční hrany jsou rovny 13. Najděte boční povrch tohoto jehlanu.

Existují také vzorce pro boční povrch pravidelné pyramidy. V pravidelné pyramidě je základna ortogonální projekce bočního povrchu, proto:

P- obvod základny, l- apotéma pyramidy

*Tento vzorec je založen na vzorci pro oblast trojúhelníku.

Pokud se chcete dozvědět více o tom, jak jsou tyto vzorce odvozeny, nenechte si to ujít a sledujte publikování článků.To je vše. Hodně štěstí!

S pozdravem Alexander Krutitskikh.

P.S: Byl bych vděčný, kdybyste mi o webu řekli na sociálních sítích.

je obrazec, jehož základna je libovolný mnohoúhelník a boční plochy jsou znázorněny trojúhelníky. Jejich vrcholy leží ve stejném bodě a odpovídají vrcholu pyramidy.

Pyramida může být různorodá - trojúhelníková, čtyřhranná, šestihranná atd. Jeho název lze určit v závislosti na počtu úhlů přiléhajících k základně.
Správná pyramida nazývá se pyramida, ve které jsou strany základny, úhly a hrany stejné. Také v takové pyramidě bude plocha bočních ploch stejná.
Vzorec pro plochu boční plochy pyramidy je součtem ploch všech jejích ploch:
To znamená, že pro výpočet plochy bočního povrchu libovolné pyramidy musíte najít plochu každého jednotlivého trojúhelníku a sečíst je. Pokud je pyramida zkrácená, pak jsou její strany reprezentovány lichoběžníky. Pro pravidelnou pyramidu existuje ještě jeden vzorec. V něm se plocha bočního povrchu vypočítá přes půlobvod základny a délku apotému:

Podívejme se na příklad výpočtu plochy bočního povrchu pyramidy.
Nechť je dán pravidelný čtyřboký jehlan. Základní strana b= 6 cm, apotém A= 8 cm. Najděte plochu bočního povrchu.

Na základně pravidelného čtyřbokého jehlanu je čtverec. Nejprve najdeme jeho obvod:

Nyní můžeme vypočítat boční povrch naší pyramidy:

Abyste našli celkovou plochu mnohostěnu, musíte najít plochu jeho základny. Vzorec pro oblast základny pyramidy se může lišit v závislosti na tom, který polygon leží na základně. K tomu použijte vzorec pro oblast trojúhelníku, oblast rovnoběžníku atd.

Zvažte příklad výpočtu plochy základny pyramidy dané našimi podmínkami. Jelikož je pyramida pravidelná, je na její základně čtverec.
Čtvercová plocha vypočítaný podle vzorce: ,
kde a je strana čtverce. Pro nás je to 6 cm. To znamená, že plocha základny pyramidy je:

Nyní zbývá jen najít celkovou plochu mnohostěnu. Vzorec pro plochu pyramidy se skládá ze součtu plochy její základny a boční plochy.

Definice. Boční okraj- je to trojúhelník, ve kterém jeden úhel leží na vrcholu jehlanu a protilehlá strana se shoduje se stranou základny (polygonu).

Definice. Boční žebra- to jsou společné strany bočních ploch. Pyramida má tolik hran, kolik je úhlů mnohoúhelníku.

Definice. Výška pyramidy- jedná se o kolmici spuštěnou z vrcholu k základně pyramidy.

Definice. Apotém- toto je kolmice k boční stěně jehlanu, spuštěná z vrcholu jehlanu ke straně základny.

Definice. Diagonální řez- jedná se o řez jehlanem rovinou procházející vrcholem jehlanu a úhlopříčkou podstavy.

Definice. Správná pyramida je pyramida, jejíž základna je pravidelný mnohoúhelník a výška klesá do středu základny.

Objem a povrch pyramidy

Vzorec. Objem pyramidy přes základní plochu a výšku:

Vlastnosti pyramidy

Pokud jsou všechny boční hrany stejné, lze kolem základny jehlanu nakreslit kruh a střed základny se shoduje se středem kruhu. Středem základny (kruhu) prochází také kolmice shozená shora.

Pokud jsou všechny boční hrany stejné, jsou nakloněny k rovině základny pod stejnými úhly.

Boční hrany jsou stejné, když svírají stejné úhly s rovinou základny nebo pokud lze kolem základny jehlanu popsat kruh.

Jsou-li boční plochy nakloněny k rovině základny pod stejným úhlem, pak lze do základny jehlanu vepsat kružnici a vrchol jehlanu se promítá do jejího středu.

Pokud jsou boční plochy nakloněny k rovině základny pod stejným úhlem, pak jsou apotémy bočních ploch stejné.

Vlastnosti pravidelné pyramidy

1. Vrchol pyramidy je ve stejné vzdálenosti od všech rohů základny.

2. Všechny boční hrany jsou stejné.

3. Všechna boční žebra jsou nakloněna ve stejných úhlech k základně.

4. Apotémy všech bočních stěn jsou stejné.

5. Plochy všech bočních ploch jsou stejné.

6. Všechny plochy mají stejné dihedrální (ploché) úhly.

7. Kolem pyramidy lze popsat kouli. Střed opsané koule bude průsečíkem kolmiček, které procházejí středem hran.

8. Kouli můžete vměstnat do pyramidy. Střed vepsané koule bude průsečíkem os vycházejících z úhlu mezi okrajem a základnou.

9. Pokud se střed vepsané koule shoduje se středem opsané koule, pak je součet rovinných úhlů ve vrcholu roven π nebo naopak, jeden úhel je roven π/n, kde n je číslo úhlů na základně pyramidy.

Spojení mezi pyramidou a koulí

Kouli lze popsat kolem pyramidy, když na základně pyramidy je mnohostěn, kolem kterého lze popsat kruh (nutná a postačující podmínka). Střed koule bude průsečíkem rovin procházejících kolmo středy bočních hran jehlanu.

Vždy je možné popsat kouli kolem jakékoli trojúhelníkové nebo pravidelné pyramidy.

Koule může být vepsána do jehlanu, pokud se osové roviny vnitřních dihedrálních úhlů jehlanu protínají v jednom bodě (nutná a postačující podmínka). Tento bod bude středem koule.

Spojení pyramidy s kuželem

Říká se, že kužel je vepsán do jehlanu, pokud se jejich vrcholy shodují a základna kužele je vepsána do základny jehlanu.

Kužel může být vepsán do pyramidy, pokud jsou apotémy pyramidy navzájem stejné.

Říká se, že kužel je opsán kolem pyramidy, pokud se jejich vrcholy shodují a základna kužele je opsána kolem základny pyramidy.

Kužel lze popsat kolem jehlanu, pokud jsou všechny boční okraje jehlanu stejné.

Vztah mezi pyramidou a válcem

Jehlan se nazývá vepsaný do válce, pokud vrchol jehlanu leží na jedné základně válce a základna jehlanu je vepsána do jiné základny válce.

Válec může být popsán kolem pyramidy, pokud lze popsat kruh kolem základny pyramidy.

Definice. komolá pyramida (pyramidový hranol) je mnohostěn, který se nachází mezi základnou jehlanu a rovinou řezu rovnoběžnou se základnou. Pyramida má tedy větší základnu a menší základnu, která je podobná té větší. Boční plochy jsou lichoběžníkové.

Definice. Trojúhelníková pyramida (tetrahedron) je pyramida, ve které tři strany a základna jsou libovolné trojúhelníky.

Čtyřstěn má čtyři plochy a čtyři vrcholy a šest hran, kde žádné dvě hrany nemají společné vrcholy, ale nedotýkají se.

Každý vrchol se skládá ze tří ploch a hran, které tvoří trojúhelníkový úhel.

Úsek spojující vrchol čtyřstěnu se středem protější plochy se nazývá medián čtyřstěnu(GM).

Bimedián nazývaný segment spojující středy protilehlých hran, které se nedotýkají (KL).

Všechny bimediány a mediány čtyřstěnu se protínají v jednom bodě (S). V tomto případě jsou bimediány rozděleny na polovinu a mediány jsou rozděleny v poměru 3:1 počínaje shora.

Definice. Šikmá pyramida je pyramida, ve které jedna z hran svírá se základnou tupý úhel (β).

Definice. Obdélníková pyramida je pyramida, ve které je jedna z bočních ploch kolmá k základně.

Definice. Akutní úhlová pyramida- pyramida, ve které má apotéma více než polovinu délky strany základny.

Definice. Tupá pyramida- pyramida, ve které je apotém menší než polovina délky strany základny.

Definice. Pravidelný čtyřstěn- čtyřstěn, ve kterém jsou všechny čtyři stěny rovnostranné trojúhelníky. Je to jeden z pěti pravidelných mnohoúhelníků. V pravidelném čtyřstěnu jsou všechny dihedrální úhly (mezi plochami) a trojstěnné úhly (ve vrcholu) stejné.

Definice. Obdélníkový čtyřstěn se nazývá čtyřstěn, ve kterém mezi třemi hranami na vrcholu je pravý úhel (hrany jsou kolmé). Tvoří se tři tváře obdélníkový trojúhelníkový úhel a plochy jsou pravoúhlé trojúhelníky a základna je libovolný trojúhelník. Apotém jakékoli tváře se rovná polovině strany základny, na kterou padá apotém.

Definice. Izoedrický čtyřstěn se nazývá čtyřstěn, jehož boční strany jsou si navzájem stejné a základna je pravidelný trojúhelník. Takový čtyřstěn má stěny, které jsou rovnoramennými trojúhelníky.

Definice. Ortocentrický čtyřstěn se nazývá čtyřstěn, ve kterém se všechny výšky (kolmice), které jsou sníženy shora na protější plochu, protínají v jednom bodě.

Definice. Hvězdná pyramida nazývaný mnohostěn, jehož základnou je hvězda.

Definice. bipyramida- mnohostěn sestávající ze dvou různých jehlanů (pyramidy lze i odříznout), mající společnou základnu a vrcholy leží na opačných stranách základní roviny.